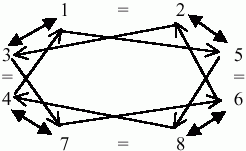
There are 8 kinds of people, whose possible relations to each other can be diagrammed like so:

Here the = signs represent possible marriages, the double-headed arrows are patrilines, and the single-headed arrows are matrilines. So, for example, someone of kind 1 is supposed to marry someone of kind 2. If the 1 is a man and the 2 is a woman, then their children are 3s; if the 1 is a woman and the 2 is a man, their children are 5s. The patrilines and the matrilines are redundant if people marry properly; a 1 man and a 2 woman have 3 children because the patriline from 1, and also the matriline from 2, point to 3. The patrilines are double-headed because not only are a 1 man's children 3s, but a 3 man's children are 1s. On the other hand, a 2 woman's children are 3s, but a 3 woman's children are 7s (and a 7 woman's children are 6s, and a 6 woman's children are 2s).
The kinship terms have three components. One tells how the types are related to each other; that is, what combinations of marriages, patrilines, and matrilines you'd have to move along in the diagram above to connect the two people. From the point of view of a 1, these components are as follows:
Finally, there's an indicator of the gender of the person referred to by the kinship term. This is a floating w for men or y for women, which attaches to the last consonant other than d, t, or l that precedes a vowel (equivalently for these words, it attaches to the first consonant in the second syllable, prior to the reduplication/infixation described above).
The answers to the questions at the end of the puzzle are:
The names are anagrams of numbers; if you take the letters indicated by these numbers from the kinship term, they spell "SYLLABIC L GOES TO M".
The family tree described in the problem is below (I've put men's names in boldface and underlined women's names; = represents marriage, again, and the lines connect sets of siblings with their parents in hopefully intuitive ways):